Research activity
Current research interests
- Neural networks (CNN, RNN, GAN, VAE, etc..)
- Signal processing
- Genetic algorithm
- Probabilistic programming
Brief introduction to Persistent homology
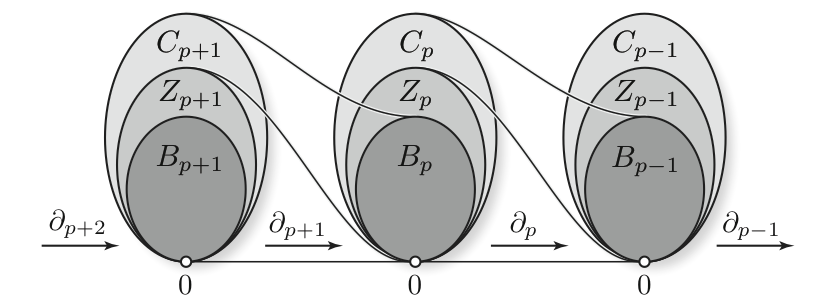
During my thesis, I worked on persistent homology. I was interested by linear representations of a specific type of quiver usually constructed from partially ordered set.
One can consider the category $(\mathbb{R}, \leq)$ composed of the reals number with their usual ordering. A functor $(\mathbb{R}, \leq) \rightarrow Vect$ with values in the category of vector spaces is then called a persistence module. The index set (source category of this functors) can also be replaced by sub-sets of $\mathbb{R}$ like $\mathbb{N}$ or $\mathbb{Z}$. This functors have a natural structure of modules over a “polynomial” ring, function of the index set. In the case of $\mathbb{N}$, the ring is $k[x]$. The name of persistence module come from this structure of module over a ring.
If we allow more dimensions by taking as index set $(\mathbb{R}^n, \leq)$ with $(x_1, \dots, x_n) \leq (y_1, \dots, y_n) \Leftrightarrow x_1 \leq y_1, \dots$, we name this construction as multipersistence. If the order of the index set alternate, like it is the case with the quiver given by $0 \leq 1 \geq 2 \leq 3 \geq \dots$, the construction is called zigzag persistence.
This functor, with values in the category of vector spaces, can be obtain by computing the homology of a filtered topological space. Hence the name persistent homology. The simplest construction consist of taking a point cloud $P \subset \mathbb{R}^m$, and then computing the sub-levelset of the (euclidean) distance function to the point cloud: $X_k = d^{-1}_P(]-\infty, k])$. This collection of sets is called a filtration. We obtain our persistence module by applying the homology functor $\mathbb{N}$ : $H(X_0) \rightarrow H(X_1) \rightarrow \dots$.
During my PhD I was looking for decomposition theorems and stability results for the signature made from this multipersistence modules.
Dissertation
I wrote my PhD at the INRIA-Saclay, Palaiseau(France) located near Paris under the direction of Steve Oudot as a member of the Datashape (former geometrica) team. My research focused on Persistence Modules and its generalization where the index set is $\mathbb{R}^2$.
Talk:
- Persistent Algebras during the JGA 2017